A VAE is a generative model used in unsupervised learning for generating new data points similar to the training data. It combines elements of both autoencoders and variational inference. In VAE the input is encoded to latent distribution z typically the normal distribution, generating the mean and standard deviation matrix. Then the sample is taken from the latent distribution z and decoded by the decoder network.
Architecture of VAE
Like the autoencoder, the VAE also consists of an encoder and decoder network. It differs from the autoencoder in terms of the encoder output. The output is the mean and standard deviation of a probability distribution typically the Gaussian.
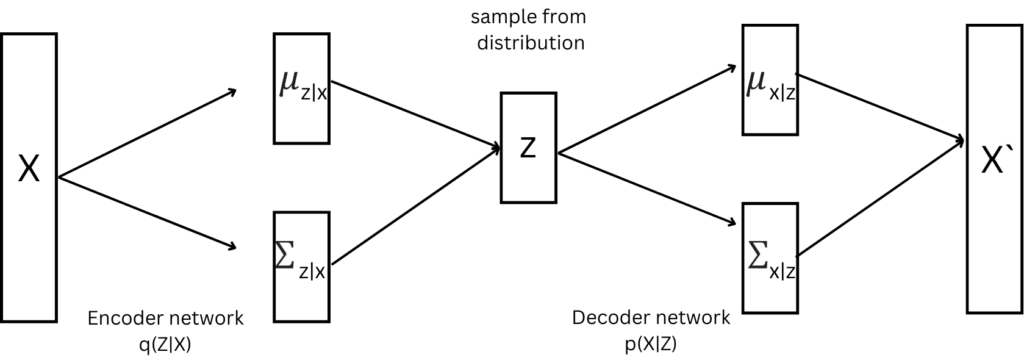
Encoder: The encoder maps the input to a probability distribution q(z|x). The output of the encoder is a mean and standard deviation vector. The mean vector defines the center around which the input sample is encoded and deviation describes how much the encoding varies from the mean.
Latent space: VAE produces the probabilistic latent space with the mean and variance. The sample is selected from this distribution.
Decoder: The decoder network samples the point from Z and the mean and variance for distribution p(x|z) are obtained. From this distribution, data is generated
Loss function:
The loss function for the VAE consists of two terms:
Reconstruction Loss:
This loss ensures that the reconstructed data closely resembles the input data. The loss function wants to maximize the likelihood of original data being reconstructed. The reconstruction loss is given as:
Reconstruction loss = E[log p(X|z)]
KL Divergence Term (Regularization):
The KL divergence term is used to regularize the latent space distribution produced by the encoder, ensuring it remains close to a prior distribution (often chosen as a standard Gaussian distribution). This regularization encourages the VAE to learn a structured and meaningful latent space representation.
KL Divergence Term=KL[q(z∣X)∣∣p(z)]
Here’s what each part represents:
- q(z∣X) is the probability distribution over the latent space given the input data X, computed by the encoder.
- p(z) is the prior distribution over the latent space, typically chosen as a standard Gaussian distribution N(0,I) where I is the identity matrix).
The KL divergence term measures how much the encoder’s distribution q(z∣X) differs from the prior distribution p(z). Minimizing this term encourages the latent space distribution to be close to the prior, facilitating better generative capabilities and disentangled representations in the latent space.
Overall Loss Function:
The loss function of the VAE combines the reconstruction loss and the KL divergence term. During training loss function is optimized to generate accurate reconstructions while learning a structured and meaningful latent space representation.
In summary, the VAE’s loss function balances the reconstruction accuracy (reconstruction loss) with the regularization of the latent space distribution (KL divergence term), leading to a model that can generate realistic data samples and capture meaningful latent representations.