Activation functions are an important part of deep learning, used to induce no-linearity in the model’s output. They enable the model to learn non-linearity in data. Without activation function, the equation of the neural network is the linear product of input values and the weights in which bias terms are added. These functions enable deep learning to perform better for the complex task that the linear functions are unable to handle.
In this article, import activation functions used in deep learning are explained with their properties and limitations.
Important Activation Functions in Deep Learning
Here the most commonly used activation functions with their properties and limitations are explained.
Sigmoid Activation Function
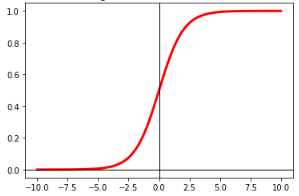
Sigmoid is a non-linear activation function used for binary classification problems. It squashes the input values between 0 and 1.
The mathematical form is given as:
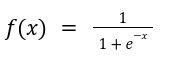
The shape of sigmoid function is shown in the below figure:
Limitations of Sigmoid
The sigmoid function suffers from the following limitations:
- The range of the activation function is between 0 and 1and it suffers from the problem of gradient kill for the large positive and negative values. The neurons are saturated for values close to 0 or 1.
- The sigmoid activation function is not zero-centred making the network training unstable and difficult.
Tanh Activation Function
The hyperbolic tangent function is similar to the sigmoid function but maps input values to a range between -1 and 1.
The equation of the tanh function is:
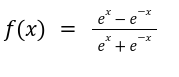
The function is shown in the figure below:
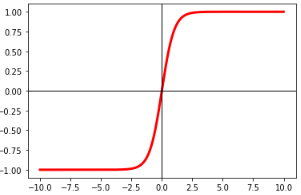
Properties
- Like the sigmoid, tanh is smooth and continuously differentiable, making it suitable for gradient-based optimization.
- Tanh function is zero-centred making it converge faster as compared to the sigmoid function during the training of the network.
Limitations
It is still susceptible to vanishing gradients for extreme input values but generally exhibits faster convergence.
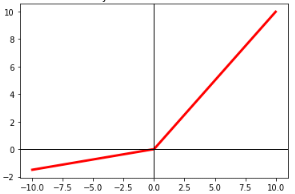
Rectified Linear Unit (ReLU) Activation Function:
ReLU has gained immense popularity due to its simplicity and effectiveness in deep neural networks. It replaces negative input values with zero and leaves positive values unchanged. Its mathematical form is given by:
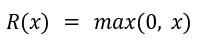
The shape of the function is shown below:
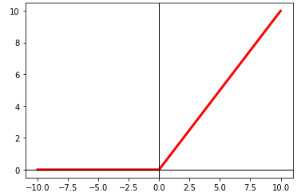
Properties
- Fast to compute and avoids the vanishing gradient problem for positive values, leading to faster training convergence.
- Introduces sparsity by zeroing out negative activations, which can aid in model generalization and regularization.
Limitations
However, when the input is negative, ReLU neurons can suffer from the “dying ReLU” problem. Neurons become inactive (output zero) for all inputs, leading to dead paths in the network.
Leaky ReLU Activation Function
Leaky relu is the modified form of the ReLU activation function, designed to deal with the dying ReLU problem. It allows a small slope for negative inputs, preventing neurons from becoming entirely inactive. The function mathematical form is:
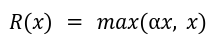
Here the parameter alpha is multiplied with input that will introduce the nonhorizontal line for the negative values. This parameter alpha does not allow ignoring the negative values, thus avoiding the dying gradient problem. The shape of the function is given as: